Un joueur lance une fléchette sur une cible. Voici les probabilités des cibles :
- Probabilité d'atteindre la cible rouge : 1/6,
- Probabilité d'atteindre la cible bleu : 1/3,
- Probabilité d'atteindre la cible jaune : 1/1,
Il mise 5 euros pour jouer au fléchettes.
S'il atteint le rouge, il gagne 20 euros, 10€ s'il atteint le bleu et rien s'il atteint le jaune.
On appelle G la variable aléatoire égale au gain algébrique du joueur.
- Probabilité d'atteindre la cible rouge : 1/6,
- Probabilité d'atteindre la cible bleu : 1/3,
- Probabilité d'atteindre la cible jaune : 1/1,
Il mise 5 euros pour jouer au fléchettes.
S'il atteint le rouge, il gagne 20 euros, 10€ s'il atteint le bleu et rien s'il atteint le jaune.
On appelle G la variable aléatoire égale au gain algébrique du joueur.
-
Donner la loi de G.
Calculons d'abord les valeurs que G peut prendre. Il y en a trois car il y a trois choix de couleurs (rouge, bleu et vert).
Pour calculer les valeurs de G dans chacun des cas, on va soustraire le coût du jeu au gain (en fonction du gain).
- Cible rouge : -5 + 20 = 15,
- Cible bleu : -5 + 10 = 5,
- Cible vert : -5 + 0 = -5,
On peut maintenant résumer la loi de probabilité de G dans le tableau suivant :
xi 15 5 -5 P(G = xi) 1/6 1/3 1/2 -
Calculer E(G).
On utilise tout simplement la formule du cours que je vous rappelle rapidement :
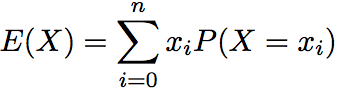
Calculons donc E(G).
E(G) = 15 × 1 + 5 × 1 - 5 × 1 = 15 + 5 - 5 = 5 6 3 2 6 3 2 3 -
Le jeu est-il favorable au joueur ?
On remarqie que E(G) > 0, ce qui signifie que le joueur est gagnant en moyenne à ce jeu. Ce dernier est donc favorable au joueur !


