Une variable aléatoire X suit la loi de probabilité représentée dans le tableau suivant :
| xi | -3 | -2 | 0 | 5 |
| P(X = xi) | 1/2 | 3/4 | 7/13 | 1/5 |
-
Calculer E(X).
On sait que l'espérance d'une variable aléatoire X est le réel :
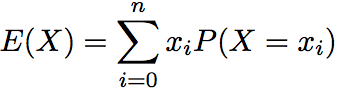
Donc ici :
E(X) = -3 × 1 - 2 × 3 + 0 × 7 + 5 × 1 2 4 13 5
E(X) = -3 - 6 + 1 2 4
E(X) = -2 -
Soit Y = X + 1. Calculer E(Y).
On sait que l'espérance est linéaire.
Comme Y = X + 1, on a :
E(Y) = E(X + 1) = E(X) + 1
Or, on a calculer dans la question précédente la valeur de E(X) qui est -2.
Donc :
E(Y) = E(X) + 1 = -2 + 1 = -1 -
Soit Z = Y + k. Déterminer k pour que E(Z) = 1.
On sait que l'espérance est linéaire.
Comme Z = Y + k, on a :
E(Z) = E(Y + k) = E(Y) + k
On cherche k tel que E(Z) = 1.
E(Z) = 1 ⇔ E(Y) + k = 1
⇔ k = 1 - E(Y)
⇔ k = 1 - (-1) = 1 + 1 = 2
Donc, pour que E(Z) = 1, k doit valoir 2. C'est aussi simple que ça.


