Théorème des valeurs intermédiaires

Cours terminale S

Voici un des grands théorèmes de Terminale. C'est absolument sûr que vous aurez une question en rapport à l'épreuve de Juin prochain.
Je vous donne le théorème, suivi de son corollaire.

Théorème

Théorème des valeurs intermédiaires

Soit f une fonction définie et continue sur un intervalle I. Soient deux réels a et b dans I.
Pour tout réel k compris entre f(a) et f(b), il existe au moins un réel c compris entre a et b tel que f(c) = k.

Corollaire

Attention, il faut absolument une fonction continue et strictement monotone sur un intervalle [a, b]. Qu'es-ce que cela veut dire ? Cela veut dire que la fonction est soit strictement croissante, soit strictement décroissante sur [a, b] et que sur cet intervalle, on peut tracer la fonction f sans lever le crayon.
Dans ces conditions là, pour tous les réels k compris dans l'intervalle [f(a), f(b)], image de l'intervalle [a, b], alors ce k admet un unique antécédent. La fonction passe obligatoirement une fois et une seule fois par ce k.

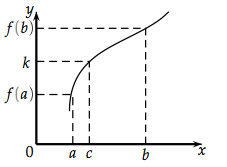
Regarde bien la figure précédente.
On a pris un intervalle [a, b] et l'intervalle [f(a), f(b)] qui n'est rien d'autre que l'image de l'intervalle [a, b].
La fonction représentée est continue et strictement monotone, en l'occurrence croissante ici.
On voit très bien que n'importe quel k compris entre f(a) et f(b) admet un antécédent par la fonction f. Vous n'avez qu'à essayer. Prenez un autre k dans l'intervalle [f(a), f(b)]. Il aura toujours un et un seul antécédent par f.

Je vais vous donner une exemple important. C'est exactement ce qu'on vous demandera de faire le jour J.

Exemple

Soit f la fonction continue définie sur [-3; 7].
On donne le tableau de variation de la fonction f ci-dessous.



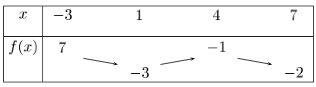
Combien de solution admet l'équation f(x) = 0 ?

• Premièrement, f est continue sur [-3; 7], comme ça on l'a dit.


• On cherche f(x)=0, donc on va chercher dans la ligne du bas du tableau de variation.

Or, 0 ∈ [-3; 7] (attention à l'ordre des nombres dans un intervalle, le plus petit d'abord). Cela correspond à l'intervalle de x ∈ [-3; 1].

• La fonction f est strictement décroissante sur [-3, 1].
• On a toutes les conditions. Appliquons le théorème des valeurs intermédiaires : L'équation f(x) = 0 admet une unique solution sur l'intervalle [-3; 1].
  Mais la question est posée sur l'intervalle [-3; 7]. Il faut donc vérifier si l'équation admet une autre solution dans l'intervalle restant, soit [1; 7].
  Regardons. Non, f(x) ne passe plus par 0. En effet, elle part de -3 jusque -1, puis de -1 à -2. Donc sans passer par 0.


• Conclusion : L'équation f(x) = 0 admet une unique solution sur [-3; 7].