On considère la fonction f définie par : f(x) = 3x³ + 2x² - 2x + 1.
-
Calculer la dérivée de f.
La fonction f est définie et dérivable sur
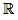comme somme de fonction dérivable sur 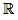et sa dérivée est : f '(x) = 9x² + 4x - 2 -
Etudier le signe de cette dérivée.
Cherchons quand es - ce que la dérivée s'annule.
f '(x) = 0 ⇔ 9x² + 4x - 2 = 0
Il faut trouver les racines de ce polynôme.
Δ = 16 - 4 × 9 × (-2) = 88
Or, √Δ = √88 = √4 × 22 = 2√22.
D'où les racines suivantes :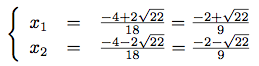
Donc : La dérivée est positive lorsque x ∈ ]-∞; x2[, négative lorsque x ∈ ]x1; x2[ et positive lorsque ]x2; + ∞[. -
En déduire le tableau de variations de la fonction f.
-
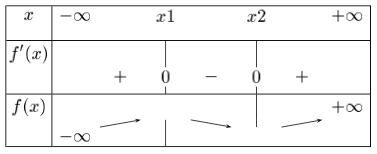
Tracer la courbe représentative de la fonction f.
-
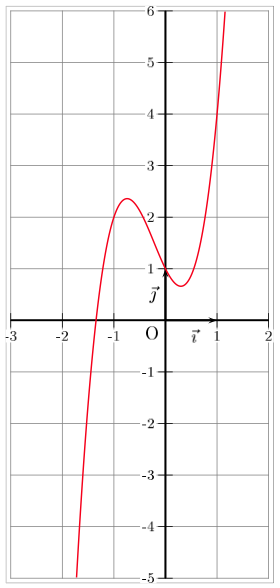
Déterminer par calcul les coordonnées du point d'intersection de cette courbe avec l'axe des ordonnées.
Qu'es-ce que cette question veut dire ?
En fait, on cherche le/les points de la courbe représentative de la fonction f qui interceptent l'axe des ordonnées, c'est-à-dire dont leur abscisse est nulle.
Notons A ce point.
On sait donc déjà que xA = 0.
Il faut donc trouver le réel y tel que : f(xA) = yA.f (xA = 0) = 3 × 0³3 + 2 × 0² - 2 × 0 + 1 = yA ⇔ 1 = yA
Donc : les coordonnées du point d'intersection de cette courbe avec l'axe des ordonnées sont : A(0; 1).
Cela se voit d'ailleurs sur la courbe précédente.