Bienvenue dans ce cours méthode dans lequel je vais vous montrer comment déterminer l'équation cartésienne d'un cercle, étape par étape, après avoir donné la propriété du cours, que vous aurez au préalable apprise par coeur !
Le but de ce cours méthode va être de déterminer une équation du cercle C de centre Ω(3; 2) et tangent à la droite (D) d'équation 3x + 4y - 1 = 0.
Calcul du rayon du cercle
Dans un premier temps, il va falloir calculer le rayon du cercle est r = d(Ω; (D)), soit la distance entre le centre Ω du cercle et la droite (D).
Je vous rappelle la formule pour calculer la distance d'un point à une droite : Soient 
la droite d'équation ax + by + c = 0, avec a et b non nuls, et A(xA; yA) un point du plan.
La distance du point A à la droite est la distance AH, avec H le projeté orthogonal de A sur .
On a :
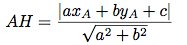
Calculons-le maintenant, ce fameux rayon.
| r = | |3 × 3 + 2 × 4 - 1| | = | √25 |
|---|---|---|---|
| 12 | 5 |
Déterminons l'équation cartésienne du cercle
A présent, nous pouvons facilement déterminer une équation du cercle C.
⇔ (ΩM² = R²)
| ⇔ (x - 3)² + (y - 2)² = | 155 |
|---|---|
| 25 |
| ⇔ x² - 6x + 9 + y² - 4y + 4 + | 144 | = 0 |
|---|---|---|
| 25 |
| ⇔ x² - 6x + y² - 4y + | 181 | = 0 |
|---|---|---|
| 25 |
Conclusion
Donc, l'équation du cercle (C) recherchée est :
| x² - 6x + y² - 4y + | 181 | = 0 |
|---|---|---|
| 25 |