Un cours méthode assez simple pour vous aider à déterminer la distance d'un point à une droite. Rien de bien méchant, il suffit juste d'appliquer correctement la formule du cours.
Le but de ce cours méthode va être de déterminer la distance du point A(2; 4) à la droite (d) : x + 2y - 3 = 0.
Rappel de la formule de la distance d'un point à une droite
Je vous rappelle (au cas où vous ne connaissez pas encore votre cours par coeur), la formule pour calculer la distance d'un point à une droite.
Soient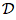 
la droite d'équation ax + by + c = 0, avec a et b non nuls, et A(xA; yA) un point du plan.
La distance du point A à la droite 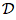est la distance AH, avec H le projeté orthogonal de A sur .
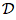On a :
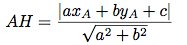
C'est bon ? Vous l'avez la formule maintenant ! Par contre, pour la suite, il faudra la connaître par coeur bien-sûr !
Détermons la distance du point A à la droite (d)
Appelons r la distance du point A à la droite (d).
Calculons :
| r = | |2 × 1 + 4 × 2 - 3| | = | √1² + 2² |
|---|---|---|---|
| |2 + 8 -3| | √5 |
Ce qui donne donc :
| r = | 7 |
|---|---|
| √5 |
Conclusion
La distance du point A(2; 4) à la droite (d) : x + 2y - 3 = 0 est :
| 7 | |
|---|---|
| √5 |
Cette distance pourra notamment servir à déterminer l'équation cartésienne d'un cercle. A garder en tête au cas où...