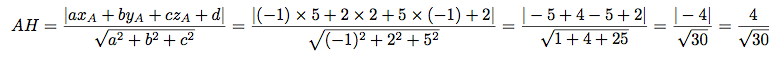Un cours sur le produit scalaire dans l'espace, avec au programme : définition, propriétés, orthogonalité, équations cartésiennes et distances dans l'espace.
1 - Définitions du produit scalaire dans l'espace
Nous attaquons maintenant la partie dans l'espace. Vous allez voir, c'est presque pareil, à un axe prés.
Définition
Produit scalaire dans l'espace
Soient
et 
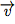deux vecteurs de l'espace.
Le produit scalaire de
et 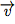dans l'espace n'est rien d'autre que le produit scalaire de et 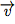dans le plan contenant ces deux vecteurs.
Prenons un point A de l'espace. Il existe donc deux points, B et C, tels que : = 
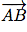et =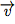 
.
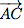Il existe forcément un plans qui contient les points A, B et C puisqu'un plan est formé par trois points distincts.
Le produit scalaire de et 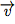dans l'espace est donc le produit scalaire de et 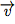dans le plan contenant ces deux vecteurs.
Pour les coordonnées des vecteurs, c'est pareil que dans le plan, à ça prés.
Définition
Coordonnées et produit scalaire dans l'espace
Soient(x; y; z) et 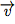(x'; y'; z') deux vecteurs de l'espace.
On a alors : . 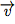= xx' + yy' + zz'
Exemple
(3; -1; 0) et 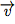(-2; 1; 5) dans l'espace.
Le produit scalaire de ces deux vecteurs est :
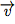. = 3 × (-2) + (-1) × 1 + 0 × 5 = -6 - 1 + 0 = -7
Et si ce produit scalaire est nul, on a aussi des vecteurs orthogonaux dans l'espace ?
Alors, oui. J'y reviens juste après ça. Ne bougez pas.
2 - Propriétés du produit scalaire dans l'espace
Les propriétés du produit scalaires dans l'espace sont les mêmes que celles dans le plan.
3 - Orthogonalité et produit scalaire dans l'espace
Nous allons maintenant parler d'orthogonalité dans l'espace.
Propriété
Orthogonalité et produit scalaire dans l'espace
Soient et 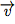deux vecteurs de l'espace.
Les vecteurs
et 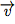sont orthogonaux si . 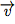= 0.
Soit un vecteur
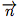de l'espace et un point A.
L'ensemble des points M de l'espace vérifiant
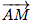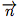. = 0 est un plan passant par A et de vecteurs normal .
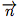Deux plans
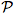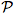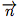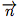et ' de vecteurs normaux respectifs et ' sont perpendiculaires si 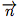.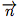' = 0.
Si on a une droite, de vecteur directeur et un plan 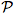, alors le vecteur est normal à ce plan s'il est perpendiculaire à toutes les droites contenues dans le plan.
Exemple
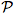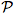et ' de vecteurs normaux respectifs 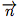(-5;0;2) et 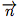'(-2; 6; -5) sont perpendiculaires.
En effet, calculons le produit scalaire de
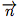et '.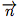
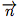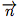.' = (-5) × (-2) + 0 × 6 + 2 × (-5) = 10 + 0 - 10 = 0Donc, les vecteurs
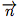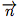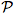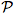et ' sont orthogonaux, et donc les plan et ' sont perpendiculaires.
Exemple
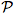passant par A(2; 3; 1) et de vecteur normal 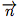(-2; 1; 3).
Pour tout point M(x; y; z) de l'espace,
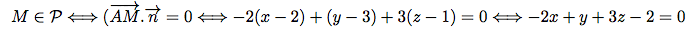
Donc, l'équation cartésienne du plan
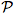passant par A(2; 3; 1) et de vecteur normal 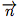(-2; 1; 3) est : -2x + y + 3z - 2 = 0.
4 - Applications du produit scalaire dans l'espace
a - Equation cartésienne dans l'espace
On va définir l'équation cartésienne d'un plan.
Définition
Equation cartésienne dans l'espace
Tout plan de l'espace, de vecteur normal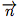(a; b; c) admet une équation cartésienne de la forme ax + by + cz + d = 0.
Réciproquement, toute équations de la forme ax + by + cz + d = 0 est l'équation d'un plan de l'espace de vecteur normal
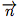(a; b; c).
Exemple
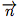(3; 0; -4).
b - Distance d'un point à un plan
On va parler maintenant de distance d'un point à un plan.
Propriété
Distance d'un point à un plan
Soient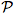 le plan d'équation ax + by + cz + d = 0 et A(xA; yA; zA) un point de l'espace.
La distance du point A au plan
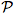est la distance AH, avec H le projeté orthogonal de A sur .
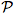On a :
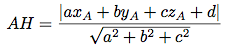
C'est la même formule que dans le plan, en rajoutant un axe, l'axe z.
Exemple
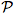le pan d'équation -x + 2y + 5z + 2 = 0 et A(5; 2; -1) un point de l'espace.
La distance de A à
est donc la distance AH, avec H le projeté orthogonal de A sur .
