Un cours méthode pour vous aider à déterminer la forme exponentielle d'un nombre complexe. Avant tout, il faut connaître la propriété du cours évidemment.
Nous allons écrire sous la forme exponentielle le nombre complexe suivant :
| z1 = | 1 + i√3 |
|---|---|
| √2 + √6 + i(√6 - 2) |
Utilisation de l'expression conjuguée
Il faut d'abord commencer par utiliser l'expression conjuguée dans le but d'enlever le i du dénominateur.
| z1 = | 1 + i√3 | = | (1 + i√3)(√2 + √6 - i(√6 - 2)) |
|---|---|---|---|
| √2 + √6 + i(√6 - 2) | (√2 + √6 + i(√6 - 2))(√2 + √6 - i(√6 - 2)) |
Développement de l'expression complexe
Développons à présent le numérateur et le dénominateur.
| z1 = | √2 + √6 + √3(√6 - √2) + i[(√3(√2 + √6) - (√6 - √2)] |
|---|---|
| 16 |
Ce qui fait, après beaucoup de calculs sans faire d'erreur (enfin, on essaie...) :
| z1 = | √2 | + i | √2 |
|---|---|---|---|
| 4 | 4 |
Factoriation
Et maintenant, on va factoriser ! Oui, mais par quoi à votre avis ? Par 1/2, oui ! On trouve :
| z1 = | 1 | ( | √2 | + i | √2 | ) |
|---|---|---|---|---|---|---|
| 2 | 2 | 2 |
Conclusion : détermination de l'expression exponentielle
Un petit rappel s'impose.
DéfinitionNotation exponentielle d'un nombre complexe
Soit f la fonction de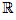
dans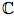 
définie par :
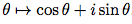
Cette fonction vérifie la propriété suivante : pour tous réels θ et θ', f(θ + θ') = f(θ)f(θ'). Cela se vérifie aisément.
Admettons que la fonction f soit dérivable. Sa dérivée est : f '(x) = -sin θ + icos θ et donc f'(0) = i.
Par analogie avec la fonction exponentielle, on écrit alors :
Soit z un nombre complexe non nul d'argument θ et de module r (arg(z) = θ et |z| = r), alors on appelle forme exponentielle de z :
Il faut donc bien connaître ses formules trigonométrique pour déterminer l'expression exponentielle, qui est :
| z1 = | 1 | eiπ/4 |
|---|---|---|
| 2 |