Vous vous demandez ce qu'est la notation exponentielle d'un nombre complexe ? Je vous dis tout dans ce cours. Définition, propriété et équation paramétrique complexe sont au programme.
1 - Définition de la notation exponentielle
Mélangeons la trigonométrie et les nombres complexes, on obtient une nouvelle notation pour un nombre complexe : la notation exponentielle.
Définition
Notation exponentielle d'un nombre complexe
Soit f la fonction de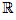 dans
dans 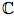 définie par :
définie par :
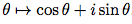
Cette fonction vérifie la propriété suivante : pour tous réels θ et θ', f(θ + θ') = f(θ)f(θ'). Cela se vérifie aisément.
Admettons que la fonction f soit dérivable. Sa dérivée est : f '(x) = -sin θ + icos θ et donc f'(0) = i.
Par analogie avec la fonction exponentielle, on écrit alors :
Soit z un nombre complexe non nul d'argument θ et de module r (arg(z) = θ et |z| = r), alors on appelle forme exponentielle de z :
Vérifions juste une chose.
Soient θ et θ' deux réels et f la fonction de 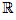 dans
dans 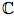 définie par :
définie par : 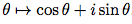 .
.
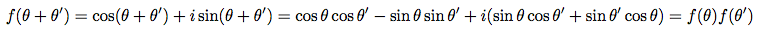
Cette propriété est relative à la fonction exponentielle.
On a donc créer une notation exponentielle pour un nombre complexe.
2 - Propriétés de la notation exponentielle
Les propriétés suivantes sont de simples propriétés de la fonction exponentielle. Vous ne devez avoir aucune difficulté à les comprendre.
Propriétés
Propriétés de la notation exponentielle
Pour tout θ, θ' ∈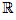 ,
,
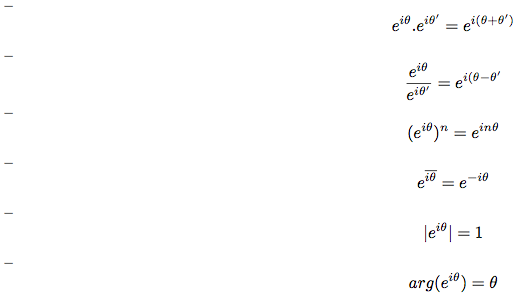
3 - Exponentielle et géométrie
Utilisons cette notation pour introduire un peu la notion de géométrie à travers la propriété suivante.
Propriété
Equation paramétrique complexe
Soient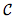 un cercle de centre O d'affixe ω et de rayon r et un point M d'affixe z.
un cercle de centre O d'affixe ω et de rayon r et un point M d'affixe z.
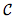 ⇔ ∃ θ ∈ ]-π; π[ / z = ω + zeiθ
⇔ ∃ θ ∈ ]-π; π[ / z = ω + zeiθL'équation z = ω + zeiθ est appelée équation paramétrique complexe du cercle
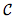 .
.
C'est normal que cela soit encore un peu abstrait pour vous.
Tachez de savoir que l'équation paramétrique complexe d'un cercle de centre O d'affixe ω et de rayon r est : z = ω + zeiθ et regardez l'exemple qui suit.
Exemple
Essayons de retrouver la forme z = ω + zeiθ.
Avec A(-1; 4).
On a bien : |z - (-1 + 4i)| = AM car l'affixe de A est z' = -1 + 4i et l'affixe de M est z. On calcul donc le module de AM en faisant : |z - (-1 + 4i)|.
L'ensemble recherché est le cercle
 de centre A et de rayon 3.
de centre A et de rayon 3.




