Commençons par calculer les affixes des vecteurs 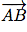 ,
, 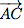 et
et 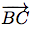 .
.
z![]() = 3
= 3
z
![]() =
= 1
-
3
i
2
2
z
![]() = -
= -5
-
3
i
2
2
Calculons maintenant les longueurs AB, AVEC et BC pour voir si, éventuellement, le triangle ABC ne serait pas isocèle.
AB = |z![]() | = 3
| = 3
AC = |z
![]() | =
| = √10
2
BC = |z
![]() | =
| = √34
2
Apparemment non, le triangle ABC n'est pas isocèle.
Peut-être est-il rectangle ? Vérifions.
AB² ≠ AC² + BC²
AC² ≠ AB² + BC²
BC² ≠ AC² + AB²
Non plus...
Conclusion : le triangle ABC est quelconque, on dit qu'il est scalène.



